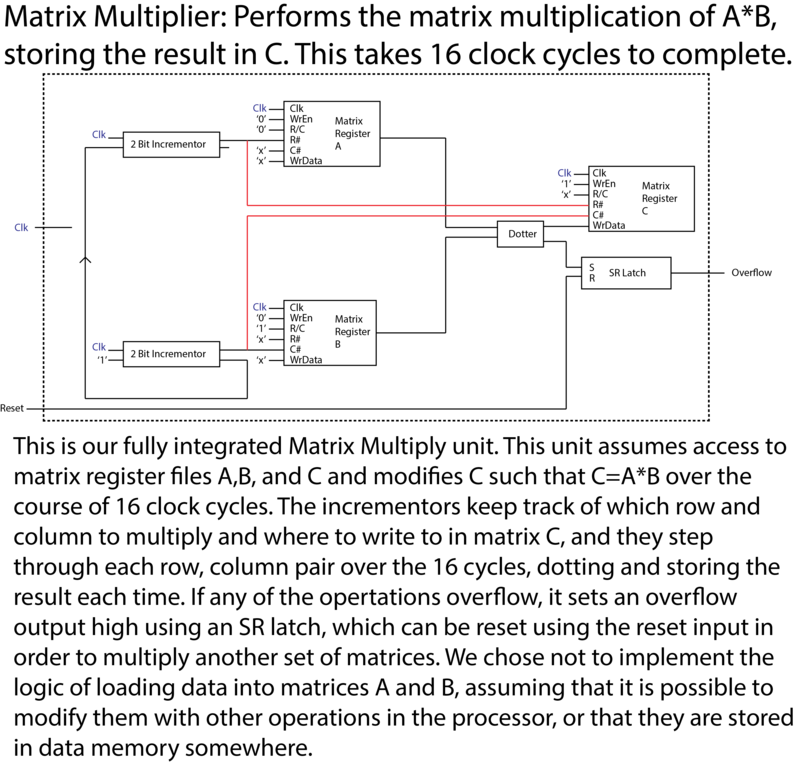
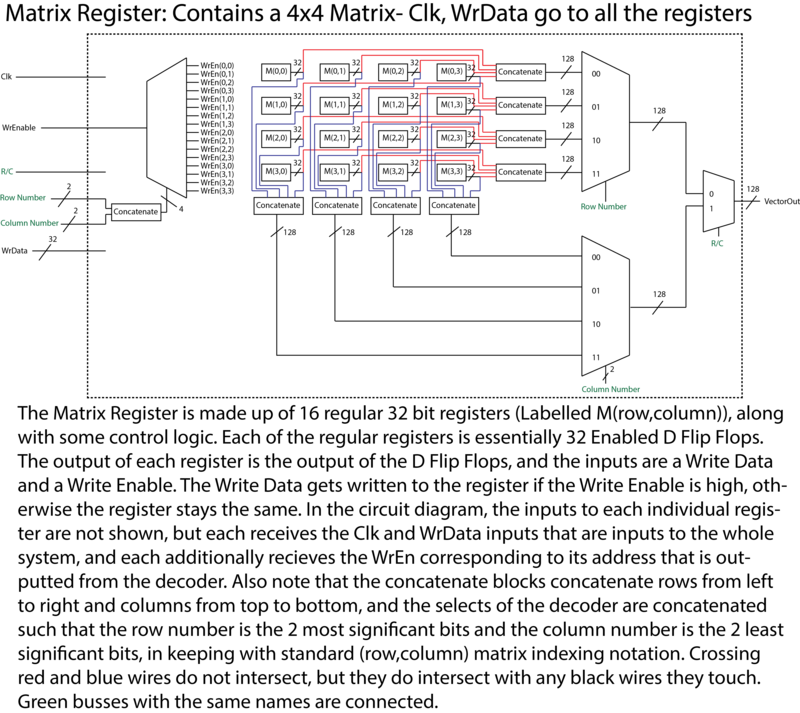
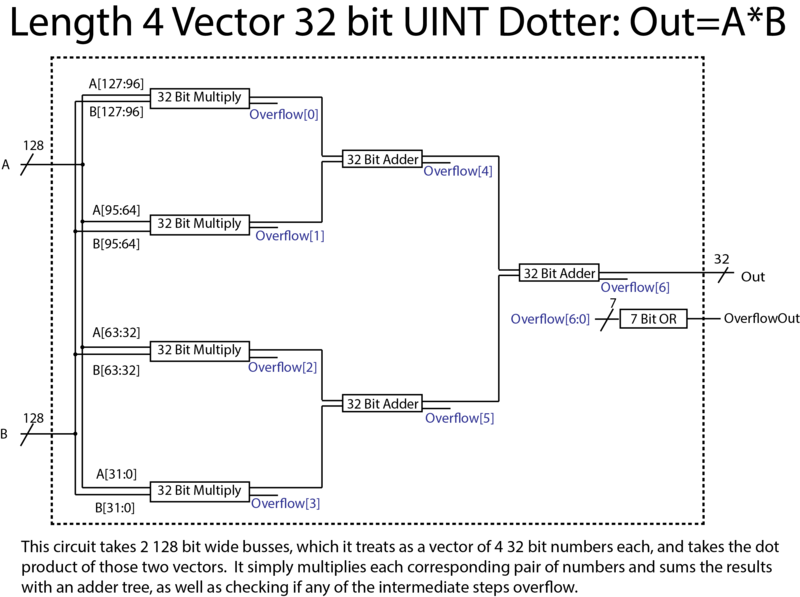
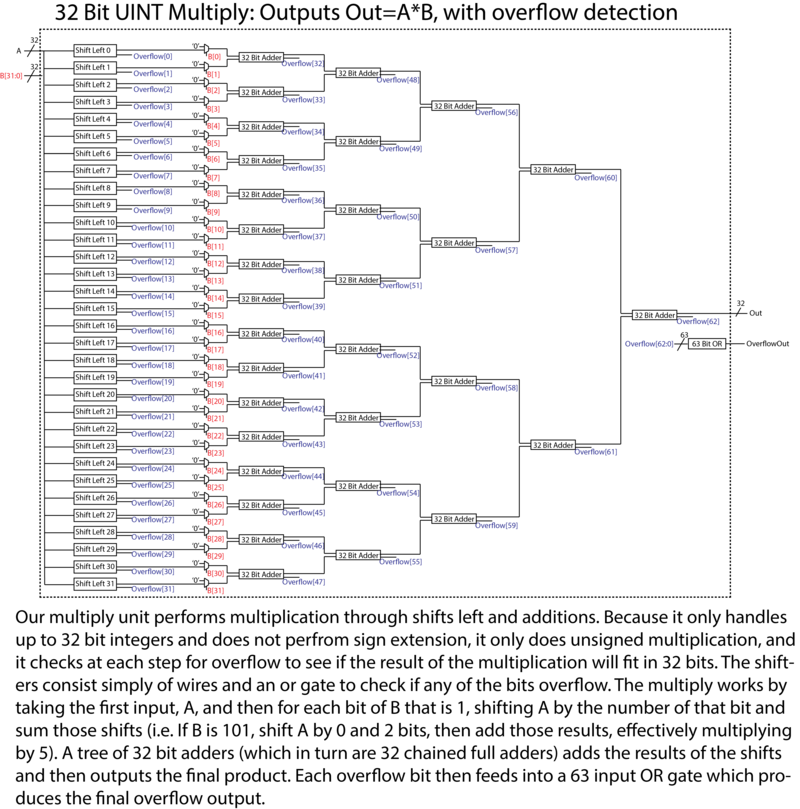
Matrix Multiplier

Gredelston and Jangowitz

Matrix multipliers!! We created a hardware implementation for a matrix multiplier, and also implemented the multiplier in assembly. In this particular case, we limited our multiplier to 4×4 matrices, where each element is a 32-bit unsigned integer; however, one could reasonably abstract to a more extensible multiplier.

Comparison of software and hardware:
We wanted to look at a hardware and software implementation of matrix multiplication to see if it is worth putting a hardware matrix multiplier into a processor in order to more easily preform linear algebra operations. Based on the size of the dedicated matrix multiplication hardware and its marginally small speed increase compared to a purely software implementation, we have determined that it is almost never a good idea to have dedicated matrix multipliers, unless that is the only operation you ever need to perform. The hardware implementation takes 16 clock cycles to compute a 4×4 matrix product, plus the amount of time to load the matrix data from memory, which should be constant with either method. The assembly code emits about 1100 instructions for the same math in MIPS, but will load the data equally fast as for the hardware, in about 32 instructions, assuming one instruction per load, giving a total of 1132 to 48 instructions. This means we only get about a speed increase of about 23x for matrix multiplication, and we are totally monopolizing 4 multiply units and 3 32 bit adders which could either be removed or used to perform other operations that are used more than matrix multiplication more quickly. Additionally, the way we are storing our matrices means we either need to use 48 registers to contain all 3 matrices at once, which is totally unfeasible given the size of most register files, or we need to be constantly loading data in and out of memory, just like a straight software implementation. Our matrix multiplier also has the issue of only multiplying 4×4 matrices, so if you have different sized matrices, it is useless, but adjusting software to handle bigger matrices is nowhere near as problematic. In the end, while designing a matrix multiplier was a fun exercise, it should forever remain just an exercise, as this is a case in which well-designed software with flexible hardware trumps large, fast, but extremely specific hardware components.

All the schematics for the hardware implementation are above – all you would need to do is actually make it in real life. The MIPS assembly implementation has been reproduced below, licensed under the WTFPL. You will need to manually input the matrices you wish to multiply, which will probably take longer than just doing the math.

#######################################
#	 4x4 MATRIX MULTIPLIER        #
# by Greg Edelston and Josh Langowitz #
#     Computer Architecture, F/13     #
#######################################

# First, let's define the two matrices that we're multiplying!!!
# The locations in data memory of the first matrix,
# as we read from left-to-right and top-to-bottom, are 9000, 9004, 9008, 9012, etc;
# and the locations of the second matrix are 9064, 9068, 9072, 9076, etc.
# (The product matrix will occupy 9128, 9132, 9136, 9140, etc.)
# Also, for simplicity of generating matrices,
# we will be performing [1,2,3,4 ; 5,6,7,8 ; etc] * [17,18,19,20 ; etc]

li $t2, 32 # We'll stop when we've inserted 32 pieces of data
li $t0, 9000 # Data memory starts at 8192, but 9000 is easier to think about.
defineMatrices:
	addi $t1, $t1, 1 # Increment the value to be stored in memory
	sw $t1, 0($t0) # Store the current value (t1) in the current location (t0)
	addi $t0, $t0, 4 # Increment the data location
	bne $t1, $t2, defineMatrices # If we haven't yet finished defining, go back.

# MAIN PROGRAM FLOW:
# 1. Initialize row and column to (0,0).
# 2. Load the first element of Matrix 1's relevant row and Matrix 2's column
# 3. Add the product of those elements to the output element.
# 4. Repeat 2-3 for the second, third, and fourth elements.
# 5. Store output element in data memory.
# 6. Increment row. If row=4, then row=0, column++. If column = 4, stop.

# 1. Initialize row and column to (0,0).
li $a0, 0 # row
li $a1, 0 # column

# 2-4...
nextElement: # ehh I'm not too happy with these label names...
	li $a2, 0 # multiplying element number
	li $v0, 0 # output element number
	
	nextSubelement: # okay I'm extremely unhappy with them
		# get the location in data memory for Matrix 1's element
		sll $t1, $a0, 4   # the row number times 16...
		sll $t2, $a2, 2   # ...plus the row number times 4...
		add $t4, $t1, $t2 # ...is the location in data memory. (other than the +9000)
		
		# get the location in data memory for Matrix 2's element
		sll $t1, $a1, 2   # the column number times 2...
		sll $t2, $a2, 4   # ...plus the element number times 16...
		add $t5, $t1, $t2 # ...is the location in data memory. (other than the +9064)
		
		# actually load the damn data
		lw $t4, 9000($t4)
		lw $t5, 9064($t5)
		mult $t4, $t5
		mflo $t5
		add $v0, $v0, $t5
		
		addi $a2, $a2, 1 # increment the multiplying element number
		bne $a2, 4, nextSubelement # if we're not already at 4, go back
	
	# figure out where we're putting this data
	sll $t1, $a0, 4  # row num times 16
	sll $t2, $a1, 2 # plus col num times 4
	add $t3, $t1, $t2 # is the location. (other than the +9128)
	
	sw $v0, 9128($t3)
	
	# increment row
	addi $a0, $a0, 1
	
	# if row = 4, then row = 0, column++
	li $t1, 4
	bne $a0, $t1, rowIsNotFour
		li $a0, 0
		addi $a1, $a1, 1
	rowIsNotFour:
	
	# if column != 4, keep going
	li $t1, 4
	bne $a1, $t1, nextElement

Additional resources:
The black boxes in our circuit diagrams do not go all the way down to the gate level. If you are not sure how the following low-level components work and want more information, check out their Wikipedia pages here:
Latches and Flip Flops: http://en.wikipedia.org/wiki/Flip-flop_(electronics)
Adders: http://en.wikipedia.org/wiki/Adder_(electronics)
Muxes and Demuxes: http://en.wikipedia.org/wiki/Multiplexor
If you have any questions about our project, contact us at jlangowitz@gmail.com or gredelston@gmail.com. Feel free to use our code or circuit diagrams for your purposes, and if for some reason you feel like actually implementing a matrix multiplier based on our schematics, please let us know how it works out.