Large Integer Hardware Exponentiation
Abstract
Exponents are a common mathematical operation. By hand, they're not too hard to evaluate. On a CPU, its fully possible to evaluate them as repeated multiplication. But what happens when the exponent is a 1000 digit number? What happens when the base is a 1000 digit number? What about both? Repeated multiplication may not be the smartest or fastest idea. It turns out there are far more efficient methods of evaluating large integer exponentiation by actually building separate dedicated hardware units. I chose to research different reasons/ techniques for doing exponentiation, and then design my own hardware exponential evaluator.
Reasoning
I choose this project because I really liked the ALU lab, but thought that it left a lot of math unexplained. How do we multiply? How do we evaluate sines and cosines? For this lab, I chose large integer exponentiation because it has extremely practical uses. RSA encryption is based on exponentiation, and requires the ability to evaluate large expressions quickly. See http://en.wikipedia.org/wiki/RSA_%28cryptosystem%29 for more info on RSA encryption. RSA encryption also makes it very valuable to have a dedicated hardware unit; computing 1000 digit exponents on a 64 bit processor would take forever!
Implementation
Software Example
Py BigNum
def expt_bin_rl(a, b):
r = 1 while 1: if b % 2 == 1: r *= a b /= 2 if b == 0: break a *= a return r
This example was the basis for my hardware implementation. I realized that the divide and modulus division of b was just a binary shift operation. From there I needed to add a few multipliers to do the math, and a basic interface for talking to the world.
My Implementation
My goals were to design an understandable hardware unit that has at least O(log(N)) computation speed with regard to multiplication (assuming multiplication can be evaluated in constant time). I wasn't going for the most optimized design ever, since there are many obscure tricks to boost speed. I just wanted better than linear time (which you get with repeated multiplication).
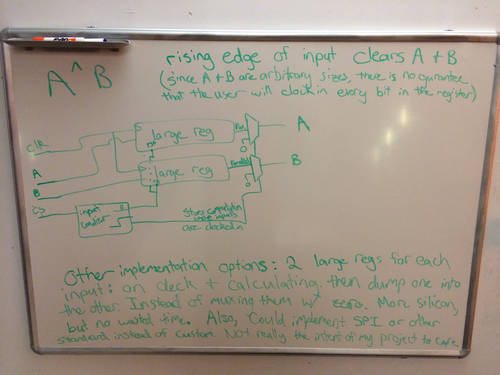
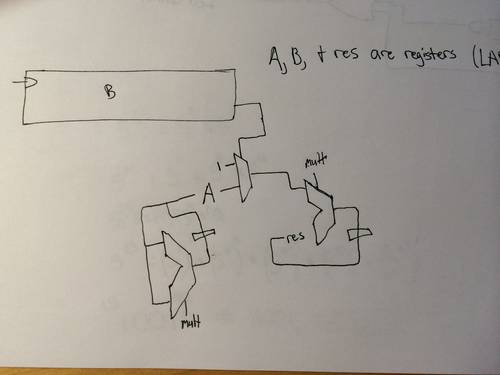
Schematics
In the top image, a basic input conditioning circuit is seen. It doesn't implement any real standard, but it gets the job done. A and B can be clocked in serially, with a chip select pin to disable computation while new values are clocked in. My implementation doesn't have a 'calculation finished' flag, but it wouldn't be too difficult to add. Instead, my implementation relies on the fact that X^0 = 1, and Y*1 = Y. Therefore, once every bit has been shifted out (so B = 0), further computations won't change the result at all.
In the bottom image, the basic computation circuit is seen. bits are serially clocked out of B, which are then used to determine if result is increased or not. If not, it is multiplied by 1. If so, it is multiplied by the 'A' register, which is equal to A^N where N is some power of 2. The 'A' register is increased each clock cycle by multiplying A by itself (giving the geometric series of A^N for N= some power of 2).
Difficulties
Although there are many examples of how to calculate exponents in Python or other programming languages, it took some time and thought to figure out how to translate this into an actual circuit. It was like learning to do math all over again, kind of like when we first did subtraction during the class. It is easy to evaluate an exponent by hand, but getting transistors to do it is much trickier.
Improvements
How do the pros do it? What other tricks are out there to go even faster? The first is modular multipliers. when taking a 1,000 digit number to the power of a 1,000 digit number, the final result will be ~1,000,000 digits long. Since most architectures have some form of ripple delay, or a large silicon penalty for avoiding the ripple delay, this can take a long time to compute. However, when looking at the algorithm presented above, the million digit number won't be present until the very end of the computation. The very first multiplication won't have more than 2,000 digits on the output. Therefore, the computation can be made faster by only using part of the multiplier for the first calculation. Modular calculation basically means having lots of cells of reconfigurable multipliers that can be turned into a single multiplier of however many bits are needed for the current operation.
There are also some interesting tricks, such as shifting to the left rather than to the right (starting with the MSB). I chose not to pursue this technique because it is less intuitive (you are calculating down rather than working your way up to the larger numbers), but can be slightly more time efficient (if you use modular multipliers) because more of your numbers will be smaller. This stems from the fact that you can avoid multiplications for any leading zeros, which are common in an arbitrarily sized exponent generator.
Continuing this Project
If another team were interested in continuing this project in the future, they could take the circuit diagrams and translate them into actual Verilog code and load it onto an FPGA. This would also require developing a hardware multiplier (something I just assumed was available). Ideally, it would be a fast multiplier, since exponents rely heavily on multiplication. They could also implement standards- my basic custom interface could be flushed out to be a full SPI interface that could talk with other devices. They could then implement the RSA standard, so that the FPGA could act as a encryption/decryption platform for some form of networking device (ie, pair it with a raspberry pie).
Work Plan Reflection
I kind of dropped the ball on this, and realized a bit late that I hadn't found a team yet. I did a bit of searching around, but most teams already had a solid start on their projects, so I decided to just work alone. Because of this late start, I didn't have much of a concrete work plan to go off of. I guess my reflection would be that next time I could benefit from a more well defined work plan (and a more timely start/ closer attention to assignment dates).